Algorithm for placing stickers on a Rubik's cube of any size

Let's try to make an algorithm. I propose an algorithm - a search in width.

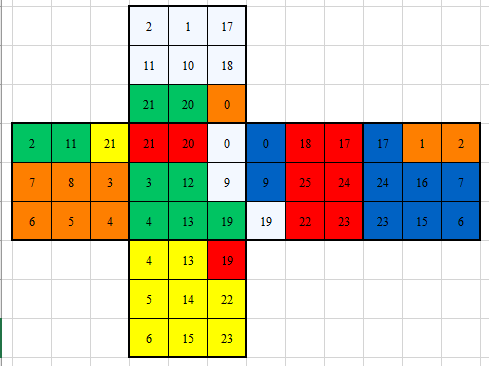
1. Let's define the object of the cube. The cube has 6 sides. 6 colors. Each side has 9 elements. Let's describe the cube as an array of 54 (6 × 9 = 54) elements. Then the ultimate goal is for every 9 elements to be equal. Let's "draw" the model.

             18 19 20
             21 22 23
             24 25 26
   0  1  2   9  10 11  36 37 38   45 46 47
   3  4  5   12 13 14  39 40 41   48 49 50
   6  7  8   15 16 17  42 43 44   51 52 53
             27 28 29
             30 31 32
             33 34 35
   

2. Let's define actions that can be done with the cube. And so, we have 6 faces, each side can be rotate around its own axis in both directions. In total, we have 6 × 2 = 12 actions. You need to describe all 12 actions. I'll describe one to you, and the rest to you. For the description-the elements will be swapped. For clarity, let's rotate the face 9-17 around itself, then I specify the elements that will be swapped in pairs:

               18     19    20
               21     22    23
               24-36  25-39 26-42
   0  1  2-26  9-11  10-14 11-17    36-29  37 38   45 46 47
   3  4  5-25  12-10  13    14-16    39-28  40 41   48 49 50
   6  7  8-24  15-9   16-12 17-15    42-27  43 44   51 52 53
               27-2   28-5  29-8
               30     31     32
               33     34     35
   

In the form of pairs, this will be the form

24-36,25-39,26-42, 2-26, 9-11,10-14,11-17,36-29,5-25, 12-10, 14-16,39-28, 8-24, 15-9,16-12,17-15,42-27,27-2 ,28-5, 29-8

20 pairs came out. 12 + 8 = 20. If the pairs are reversed , there will be a rotation in the opposite direction. Such pairs of 20 pieces should be 12 options. I show you one.

I will try to describe the rotation of the drawings in 3D. The rotation will only occur for 9 elements, from 9 to 17 including 13. The rest will not rotate if it is a 2D projection, and already translating this into a 3D projection, we will get more options.

Packed u-turn option a[i] = (a[i] & 7) + ((a[i] + 8) & (8+16)) and left a[i] = (a[i] & 7) + ((a[i] - 8) & (24)) apply this for the 9 elements after the permutations. Then (a[i] & 24) = {0,8,16,24} depending on the reversal.

The U-turn option is simple with and x.size = (x.side+1)&3 or x.size = (x.side-1)&3

The U-turn option is complicated if (x.size=3) x.size = 0; else x.size++ or if (x.size=0) x.size = 3; else x.size--

UPD Important: when performing a rotation operation, it is better to create a separate array, since it is possible to" accidentally " assign a single cell twice. For example, at 11, we assigned 9, and at 17, we assign 11 - and we get a "failure", so on the left from the assignment should be the original array, and to the right (where we attach) - a duplicate of the original array.

BOTTOM LINE: we do 20 permutation operations, then 9 2D rotation operations, and one of the 9 is the central element that is not included in the 20.

1. Having the object of the cube, let's define the final condition: it will be o[0]=o[1]=...=o[8], o [9]=o[10]=...=o[17],..., i.e. all every 9 elements of the array must be equal.

2. Now, when we have an "object", we create an array of objects, and start building a tree. Each new level adds several elements to the array. This is necessary in order to remove the "extra" movement, and find a solution using the search in width.

   We make the structure (iteration number, action number(1-12), element number that led to the appearance of this object, "object" (array on 54)) Then we build the 1st iteration, i.e. a cycle of 12 permutations of faces, we get

    a[0]=(0,0,0,-1,obj),a[1]=(1,1,0,obj),a[2]=(1,2,0,obj),a[3]=(1,3,0,obj),
    a[4]=(1,4,0,obj)..a[12]=(1,12,0,obj);
   

   We check each object condition [3]. Making the 2nd iteration. There will already be a problem. Duplicates will start appearing. Duplicates are formed when we rotate the same face first to the left, and then on the 2nd iteration, to the right. You can figure out how to avoid this algorithmically, but it is difficult. In addition, you also need to filter 4-fold rotation, etc., so it's easier to just filter duplicates. Ie, as for me, it's easier to check with the addition of a new array element - whether there are duplicates below, in the elements a[0]…a[n] (a[12]). The second iteration will bring 12 × 12 = 144 elements, but half of them will be exactly duplicates. So there will be somewhere +72 elements. To simplify it, let's do this. The second level will look something like this

    a[0]=(0,0,0,-1,obj),a[1]=(1,1,0,obj),a[2]=(1,2,0,obj),a[3]=(1,3,0,obj),
    a[4]=(1,4,0,obj)..a[12]=(1,12,0,obj);
    a[13]=(2,1,1,obj),a[14]=(2,1,2,obj)...a[84]=(2,12,6,obj)
   

Then we repeat the iterations until a solution is found (i.e. the condition [3] is not met. The array can be used to set the course of events (i.e., if the answer is 84, then 84 gave rise to element 6, which gave rise to element 0. in element 6, it is specified where rotated).

P.S. In 3D rendering, there will be 6 × 4 = 24 positions of the drawing. If the rendering is smooth, then you will need to move smoothly from one of the 24 positions to the other. The square can be pasted on the cube in 4 ways.

The cube has 6 sides, so for 3D-you have 24 variations. But if you operate with 24 options, the task of rotation becomes more complicated, because you will have to rotate all 20 elements (20 pairs of [2]). It is easier to spin 9 elements with 4 combinations, and add +6 combinations in the 3D rendering phase (6-depending on which side of the cube we are on). That is, when rendering, there will be realside = side+ kubeside* 4 where size is the value of one of the 54 elements, size is within [0..3], and kubeside is within [0..5] - means which side of the cube we are on. After projecting onto the 2D space, it may turn out that these 24 options have moved to 12 or less, but it is the number 24 that gives the basis that "removes" the chaos. I.e., sets the order such that the face cannot be expanded "not". there."

It seemed to me that about 24 combinations is not quite clear. I'll try to draw

        ^ ^ ^
        < ^ v
        > > > 
 < ^ >  ^ ^ >  ^ ^ ^  > > >
 < v >  v v >  ^ < <  < ^ v
 < v >  ^ ^ v  < < <  v v v
        < < >
        ^ ^ >
        V V V

This is a combination of 4 positions on a two-dimensional scale. It will be multiplied by 6 options, because each of the 6 sides will have to be rendered in 3D in 6 ways. And the 3D model will be... you need to think about what you can quickly draw… It means that the combination 0..53 × 4 варианта развотота × 6 вариантов нахожнения на стороне will always give a uniquely 3D vector. 0..53 will give unambiguously the 3D coordinate of the vector, and 24 (4 × 6) gives the u-turn, the direction of the vector Three-dimensional. I.e., you can create an array of 54 coordinates, and 24 directivity vectors - and the 3D transformation will go smoothly.

I paint 24. In 2D, we will have 4 plane vectors: 0, 90, 180, 270 (rotation in the XY plane).

In 3D, the following turns will overlap (XY, XZ, YZ).

  ^y           2 (0,0,90)
  0(0,270,0)   1 (0,0,0)   4(0,90,0)  5(0,0,180)
               3 (0,0,270)        --x>

I hope I correctly described the rotation vector in degrees. Adding (0, 90, 180, 270) to the first rotation coordinate XY-we get 24 combinations of turns.

5th (back) - controversial, if it is expanded by 180 on XZ and even by 180 on YZ-then we get the "original position of the object" in almost "mirror form". 5(0,180,0) I can't say whether it is correct 5(0,180,0) or so 5(0,180,180) or so 5(0,0,180).

Acceleration. Since the cube is meaningless to twist one side left-right, etc., you can add conditions to the cycle for 12 that prohibit doing this. For example, so

   if (level >= 2) /*then*/ {
      if (( a[a[i].prev].turn & 14 ) == (turn & 14)) /*then*/{ 
         // Если предыдущую грань двигали  ту же самую
         if (a[a[i].prev].turn != turn )  /*then*/
            continue; //Если Если предыдущую грань двигали в другую сторону
         // то не рассматриваем дальше, убрать туда-сюда движение
         // сюда код прийдёт, если более одного раза двигаем одну грань   
         if (a[a[a[i].prev].prev].turn == turn)
            continue; // Запрет поворачивать третий раз куб в одну сторону                      
      }

That is, in the end, the algorithm will be as follows.

1. Setting the initial value condition
2. Start of iterations, cycle for 12 movements
3. Check the conditions for unnecessary movements, if there are any-go to 2.
4. Perform the movement, prepare a '
5. We check the "boundary condition" that the cube is "assembled". If collected , the solution is found.
6. We check that a' is missing in the array a. If present-to n 2.
7. add a' to the array, and go to 2.
8. At the end of the loop, we create another iteration.

By reading about the Rubik's cube in Wikipedia, I found an entry that in 20 moves you can find a solution. It may be more efficient to search deep with a limit of 20. For such a search, you will need an array of 20, and not several thousand, as in this version.