How does the AES encryption algorithm work?
I would like to understand how the encryption algorithm works AES (Advanced Encryption Standard). I am looking for didactic answers, that make me understand the processes used by the algorithm step-by-step, emphasizing the logical and mathematical part, and if possible, the operations with bits.
Note that I do not ask for code examples, although they are valid for the explanation.
3 answers
AES is a cryptographic primitive intended to compose symmetric encryption and decryption systems (i.e. the same key for encrypting and decrypting). It is a block cipher, that is, it operates in blocks of fixed size (128 bits, or 16 bytes). Like any block cipher, it can be transformed into a stream cipher (so as to operate on data of arbitrary size) through a mode of Operation, but this does not come to the case here. It can work with 128, 192 or 256-bit keys (o Rijndael algorithm, which originated the AES, allows more key sizes).
In other words, it is an algorithm whose direct function (encryption) receives as inputs a block of 128 bits (the message) and a key of the chosen size, and returns an output also of 128 bits (The Cipher). The inverse function (decryption) receives as input a 128-bit block (the cipher) and returns as output a 128-bit block. If the key is the correct key, this output is identical to the message original.
The purpose of a successful cipher is that it is impractical if you discover the original message if you only have the encrypted message, but not the encryption key. To do this, we seek to minimize any visible correlation between the input and the output, so that the same (and/or the key) can be deduced simply by observing a very large number of ciphers (or message/cipher pairs). To do this, a series of "rounds" (or rounds) is used in which the bytes undergo nonlinear, but reversible transformations (i.e. to decipher, simply perform the inverse of the same operations, in reverse order).
Finite Bodies
All operations in AES treat the input bytes as a finite body ( finite fields , or Galois fields ) in 28. This means that:
- there is a set
[0,255](which are all possible values for a byte) and one of these elements is called "zero" (in the case, the0); - there is an operation, which we will call "addition", which applies to any two elements in this set and whose result is also an element of this set. This operation needs to be associative, commutative, have a neutral element, and each element must have an inverse;
- in this case, we define the " addition "as the" or exclusive " - XOR.
- there is an operation, which we will call "multiplication", with characteristics similar to the "addition". Except for the element "zero", which has no inverse (and the neutral element of multiplication is called"one"). Multiplication also needs to be distributive with respect to addition.
- the "multiplication" will be defined below.
For those who do not have experience with mathematics, it is good to emphasize that we are defining "addition", "multiplication", "zero" and " one " - these names do not necessarily have anything to do with operations usual arithmetic we do in the set of natural or real numbers (the natural or integers, for example, do not form bodies with the usual + and *, since there is no x within these sets such that 2*x=1; The Real Ones form a body, only infinite). There is no "subtraction", "division", etc.
Addition, as already said, was defined as being the XOR. Multiplication is more complex: first treat each operand as if it were a polynomial based on its representation binary (ex.: 6 - 110 - turn x^2 + x, and 11 - 1011 - turn x^3 + x + 1), multiply them, then divide the result by a"reducing agent". The rest of the division (interpreted again as a number) will then be the result of multiplication. In the case of AES, the reducing agent chosen was:
x^8 + x^4 + x^3 + x + 1
So multiplying 6 by 11 is the same as doing
(x^2 + x)*(x^3 + x + 1) mod (x^8 + x^4 + x^3 + x + 1)
=[(x^5 + x^3 + x^2) + (x^4 + x^2 + x)] mod (x^8 + x^4 + x^3 + x + 1)
=(x^5 + x^4 + x^3 + x) mod (x^8 + x^4 + x^3 + x + 1)
=111010 mod 100011011
=111010
=58
Note that coefficients are "summed" using XOR, not the common sum: when adding x^2 with x^2 the result is zero , and not 2*x^2. Think of this sum as 1*x^2 + 1*x^2 = (1 xor 1)*x^2 = 0*x^2 = 0. The body GF(2^8) was built on the basis of the GF(2) (binary body, where the sum is XOR and the multiplication is AND), so that its polynomials have only 0 or 1 as coefficients. For more details, the English Wikipedia has an article on arithmetic in finite bodies , including a specific subsection on Rijndael.
Wikipedia has a algorithm simplified which is equivalent to this multiplication of polynomials, but much less expensive (see at the end of the section).
That is, a [unoptimized] implementation of AES could for example create a distinct data type to represent each byte of the inputs/outputs/keys and give its own implementation of "addition" and "multiplication" (overloading the usual ones, if the programming language allows). This would simplify the logic, at the expense of performance.
big disclaimer: not I'm suggesting that lay people implement AES [to use in practice] - I don't trust myself to implement cryptographic algorithms, let alone anyone reading this... I put this only for didactic purposes, a real implementation needs to worry even about things like side channel attacks (ex.: timing e foul).
- Note: A from now on, whenever I talk about "ADD" or "multiply" I mean operations in GF(28), unless otherwise indicated.
Rijndael S-Box
Based on this finite-body arithmetic, a Lookup table (lookup table) called Rijndael S-Box was designed, intended to transform one byte into another, in a nonlinear way. Two tables are used: one for the direct function and the other for reverse.
First, the multiplicative inverse of the byte is calculated (i.e. a byte such that multiplied by it results in "one"). Zero has no inverse, so it maps to zero itself.
-
Then the eight bits of the result are subjected to a affine transformation , to make the method more resistant against algebraic attacks :
[1 0 0 0 1 1 1 1][b0] [1] [1 1 0 0 0 1 1 1][b1] [1] [1 1 1 0 0 0 1 1][b2] [0] [1 1 1 1 0 0 0 1][b3] + [0] [1 1 1 1 1 0 0 0][b4] [0] [0 1 1 1 1 1 0 0][b5] [1] [0 0 1 1 1 1 1 0][b6] [1] [0 0 0 1 1 1 1 1][b7] [0]
This table was designed to be resistant to cryptanalysis linear or differential, and allowing the substitution of the Affine transformation by another if one discovers any backdoor in the future. For practical purposes, it is an invertible function whose output does not resemble the input at all (i.e. small changes in the input produce seemingly random differences in the output).
Key expansion
As said, AES has several calculation rounds, which part of the message original, applies a series of transformations in it, and comes to the final result (the cipher). I will call the data being worked "State" (state):
estado = mensagem
estado = round(estado)
estado = round(estado)
estado = round(estado)
...
estado = round(estado)
cifra = estado
In each state, one does not use the original encryption key, but rather a series of keys derived from it. This derivation uses an algorithm called Rijndael Key Schedule, and is complex in itself to be fully explained here (although the implementation is apparently short). Give just an overview, therefore:
- AES operates in 128-bit blocks, as seen, but uses 128, 192, or 256-bit keys; the key expansion algorithm therefore produces a set of 128-bit subkeys - one for each Round of the algorithm (which by the way also depends on the key size: they are 10, 12, or 14 rounds, respectively).
- starting from the original key, a series of operations are performed involving the rotation ( shift ) of the last 4 bytes, its transformation according to the S-Box, and the addition with a power of 2. There is a small variation in the steps depending on the key size used.
- by "power of 2", I mean 2 multiplied by itself N times, in GF(28). As you can see in this table , the values are quite different from integer arithmetic.
- once sufficient bytes have been produced for all rounds of the algorithm, a expansion of the key.
Rounds
The algorithm works in rounds, or rounds, so that in each of them a series of reversible operations is done on top of the state. The goal is that each byte of the input is "combined" with several bytes of the key, so that small changes in both the key and the message cause significant changes in the cipher (see confusion and diffusion). In other words, if you want to avoid that part the cipher depends only on part of the key, which would break the problem of deciphering a large key in decrypting several smaller keys (which could be done by brute force).
Note: state bytes are commonly represented in a 4x4 array. This array is per column, not per row (as in most popular programming languages). That is, the 16 bytes are arranged as follows:
b0 b4 b8 b12
b1 b5 b9 b13
b2 b6 b10 b14
b3 b7 b11 b15
When "row" or "column" is mentioned", refers to the 4 bytes of the state corresponding to the above representation.
-
In the first round, the state is added to the key of that round;
estado = estado ^ chave(0) -
In subsequent rounds:
-
Each byte of the state is transformed according to the S-Box;
para cada byte b no estado: estado[b] = S(estado[b]) -
Then the rows are rotated to the left, as follows:
a00 a01 a02 a03 <<0 a00 a01 a02 a03 a10 a11 a12 a13 <<1 a11 a12 a13 a10 a20 a21 a22 a23 <<2 a22 a23 a20 a21 a30 a31 a32 a33 <<3 a33 a30 a31 a32 -
Then in each column of the array its bytes are combined with all other bytes in the same column; this step does not occurs in the last round.
The detailed description of this step can be seen here . What is done is to take each column of the Matrix and multiply it by a fixed Matrix, resulting in the new column values:
[a00] [2 3 1 1][a00] [a10] = [1 2 3 1][a10] [a20] [1 1 2 3][a20] [a30] [3 1 1 2][a30] a00 = 2*a00 ^ 3*a10 ^ 1*a20 ^ 1*a30 a10 = 1*a00 ^ 2*a10 ^ 3*a20 ^ 1*a30 a20 = 1*a00 ^ 1*a10 ^ 2*a20 ^ 3*a30 a30 = 3*a00 ^ 1*a10 ^ 1*a20 ^ 2*a30 ... (idem pras demais colunas)By my understanding, multiplication remains multiplication in GF(28), but in this case there is a simpler description of it:
x*1 é x,x*2 é x<<1andx*3 é x<<1 ^ x. If the result is greater than255, Dox ^ 0x1B. -
Finally, add the key of the round to the state.
estado = estado ^ chave(i) # onde i é o número da rodada
-
Summary
This series of operations (add key, replace, mix/swap) is called "Substitution-Permutation Network", or SP-network. Here is a graphical representation of the process, with 3 rounds :
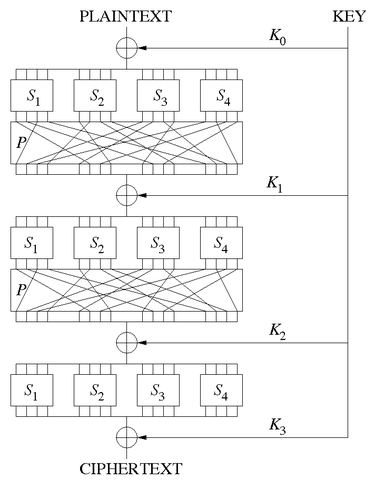
Deciphering
The process of deciphering consists simply in the application of the inverse of these same operations, in the inverse order of course. Often nothing changes between encrypting and decrypting (e.g. a xor b xor b = a), in others some adaptation is required:
Instead of starting with
estado = mensagemand ending withcifra = estado, we now start withestado = cifraand end withmensagem = estado;The expansion of the key is equal; at the beginning of each Round the corresponding round key is added (Remembering that we are now doing the rounds back to front), and at the end we add the key of the first round;
-
To undo Step 3 (mixing columns) of each Round in which it applies (i.e. all except the first and last), the inverse matrix to the one described above is used:
[a00] [14 11 13 9][a00] [a10] = [ 9 14 11 13][a10] [a20] [13 9 14 11][a20] [a30] [11 13 9 14][a30](since this time there are no "shortcuts" for multiplication, it is common to use another lookup table instead of doing the it counts on time. here has the relevant tables.)
Step 2 is simply a shift to the right instead of the left...
To undo Step 1, use a lookup table that corresponds to the inverse of the S-Box.
First of all, my answer only intends to add content to the answer of mgibsonbr, which is already quite complete. I had to make a theoretical rationale for my course completion work. I think it would be very selfishness of me, to leave everything I wrote only on paper, so therefore I decided to share what I wrote with the community. Some improvements are still needed and I think I may have made some slips, because the algorithm is very much complex. If this happens, feel free to edit my answer.
1-cryptography
Second Bond et al. (2003), encrypting data means converting it so that it can only be decrypted and read by authorized users, therefore, data encryption requires an algorithm to be applied to this data. The way to write logic is called an algorithm, which, according to Cormen et al. (2002, p. 3), nothing is more than any computational procedure as well defined that takes some value or set of values as input and produces some value or set of values as output. Therefore, an algorithm is a sequence of computational steps that transform input into output. In this way, an encryption algorithm is a mathematical procedure that contains an input, the data to be encrypted, performs a processing mathematical based on a key, and generates an output: the encrypted data (KUROSE; ROSS, 2010; BOND et al., 2003; RAPPAPORT, 2009; STALLINGS, 2008; FOROUZAN; FEGAN, 2008). Forouzan and Fegan (2008) explains some terms used when referring to cryptography, according to him:
- Cipher: are the encryption and decryption algorithms
- Key: is a number or set of numbers over which the cipher operates.
2-Symmetric Cryptography
Symmetric encryption is the type of encryption that uses the same key to encrypt and decrypt data (FOROUZAN; FEGAN, 2008). Generally symmetric encryption algorithms are quite sophisticated and use 56 or 128-bit keys. Due to the size and mathematical probability of the number and complexity of the key, an encryption algorithm cannot be easily reversed, this means that without the key, the encrypted data would take hundreds of years to be deciphered in a brute force attack, that is, if, only if, the algorithm that encrypted this data is sufficiently robust (BOND et al., 2003).
Symmetric encryption is used to ensure the confidentiality of certain data and ensures that only authorized recipients, those who know the decryption key, can retrieve the original data (BOND et al., 2003).
An example of symmetric encryption is the AES algorithm, from English: Advanced Encryption Standard, which is an evolution of DES and was developed because the DES key was too short. The AES is a very complex cyclic cipher and was designed with three key sizes: 128, 192 or 256 bits (Forouzan; FEGAN, 2008).
3-Asymmetric Encryption
Asymmetric encryption is one that uses different symmetric encryption algorithms and requires the use of two keys: the private key, which is kept secret by the owner and used to encrypt data, and the public key, which is known to persons authorized by the owner of the private key and is used to decrypt the data (FOROUZAN; FEGAN, 2008). However, if a data is encrypted with the public key, only the owner of the private key can decrypt this data (BOND et al., 2003)
4-The AES algorithm
The advanced encryption standard algorithm, or simply AES, is a 128-bit (16-byte) block symmetric encryption algorithm, developed since 1997 by Vincent Rijmen and Joan Daemen, and announced on November 26, 2001 by the NIST, (National Institute of Standards and Technology) Institute US National Standards and Technology in free translation (NIST, 2001)1.
The AES algorithm has 128-bit, 192-bit or 256-bit keys or 16, 24 and 32 bytes respectively. Key is understood as the digital data set on which the cipher operates (Forouzan; FEGAN, 2008). Because it is a symmetric encryption algorithm with 128-bit blocks, the encryption function, which is the function responsible for transforming and shuffling the data, receives blocks of 16 bytes (128 bits) at a time and returns, too, 16 bytes per time. It is called the set of blocks that will be encrypted "message", and the set returned by the encryption function"cipher". The decryption process is done analogously, however, contrary to that of encryption and therefore receives a set of encrypted blocks (cipher) and returns the message identical to the original, if, only if, the key is the same as it was used to encrypt the data. The encryption process can also be called encryption or even "encryption", in the same way that the decryption process is synonymous with"decryption "or"decryption" (NIST, 2001). Figure 1 shows a pseudocode of the AES algorithm, the steps of the algorithm are explained later.
Figure 1-AES Pseudo code
Source: adapted from NIST (2001, our translation)
5-The State
Internally, the operations of the AES algorithm are performed on a two-dimensional array of bytes "State" calls (s). The state consists of an array organized in 4 columns of bytes, each containing 4 bytes, 16 bytes in all, and the values of each byte range from 0 to 255. During the encryption or decryption process, 128-bit blocks (16 bytes) are copied to this array, so that responsible operations are performed by the functioning of the algorithm in this copy (NIST, 2001). Figure 2 illustrates the input blocks, the State array, and the output blocks, with each item corresponds to one byte:
Figure 2-input blocks, State and output blocks
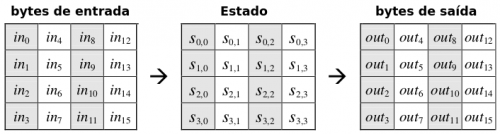
Source: adapted from NIST (2001, our translation)
6-addition Operation {
Addition is nothing more than a sum of the bits, known as the XOR operation (or Exclusive), also called "exclusive disjunction". It is a logical operation between two operands that results in a true logical value if, and only if, exactly one of the operands has a value true. It can be synthesized as a detector of differences between two logical operands (NIST, 2001) and is represented by ions.
7-multiplication Operation {
In the case of the AES algorithm the multiplication is the polynomial representation GF(28) (indicated by⊗), that is, corresponds to the multiplication of modulo polynomials in irreducible polynomials of degree 8. A polynomial is irreducible if its only divisors are one and itself (NIST, 2001, our translation). For the AES algorithm, this irreducible polynomial is: 2
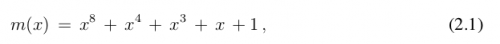
Or {01} {1B} in hexadecimal notation.
For example, 57 ⊗ 83 = c1, because:
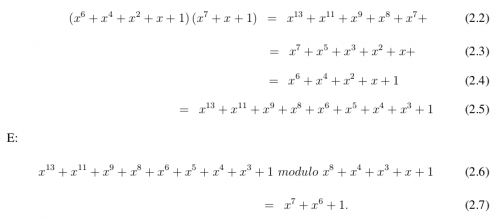
X7 + x6 + 1, the obtained result, it can be written as7 + x6 + 0x + 0x + 0x + 0x + 0x + 1 is: {11000001} in binary is equivalent to {c1} as a hexadecimal value.
The 2x agents2 and 2x were cut because these polynomials only they have 0 and 1 as factors, so even factors saw 0 and odd factors saw 1.
The modular reduction by m (x) ensures that the result will be a polynomial binary of degree less than 8, and thus can be represented by a byte. On the contrary, there is no simple operation at the byte level that corresponds to this multiplication (NIST, 2001, translation ours)3.
Therefore, in a simple way, it is understood that the multiplication operation is the representation of the polynomial in its binary representation, made a multiplication of the agents of this equation and subsequently divided by the reducing agent (modulus operation). The rest of this division will then be the result of the multiplication operation. In the case of AES, the reducing agent cited in Equation 2.1
8-Rijndael S-Box e A Subbyte Step
The Rijndael S-Box, or simply S-Box, is a square, nonlinear matrix used as a replacement table in several byte transformations. It is also used in routines of expanding one-to-one value keys in bytes. In the AES algorithm it is used in the Subbyte step and during key Expansion)4 (NIST, 2001, our translation).
The Subbyte step, or subbyte transformation, is a nonlinear substitution that operates independently on each byte of the state array using the Rijndael s-Box substitution table (NIST, 2001, translation ours). To Rijndael S-Box is reversible, and is built by composing two transformations5:
- the multiplicative inverse of the byte is calculated, i.e. a byte such that multiplied by itself, it results in 1. Element 0 (zero) is mapped to itself.
- applies an affine transformation, which can be expressed in matrix form as:
Related transformation of the Rijndael s-Box
Source: adapted from NIST (2001)
During the SubBytes, the bytes of the State array are overwritten from the S-Box, generating different and seemingly random values. The S-Box used in this step is shown in Figure 3.
Figure 3-s-Box in hexadecimal notation
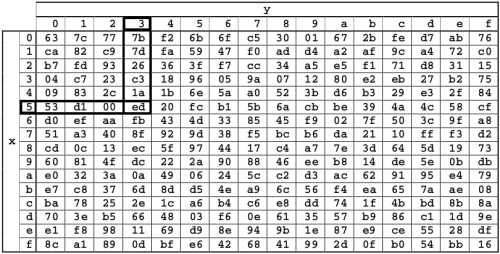Source: adapted from NIST (2001)
For example, if we have the position State1,1 = {53}, then the value of the substitution will be determined by the intersection of the index row 5 and Index column 3, Illustrated in Figure 3. I.e., the result of the substitution in the state position1,1 it will be {ed}.
9 - ShiftRows stage
In the ShiftRows step, the bytes of the last three rows of the state are shifted cyclically along different numbers of bytes (offsets) 6 (NIST, 2001, our translation). Only the first row, it is not shifted. Figure 4 illustrates this process and highlights the bytes that have been transposed.
Figure 4-step ShiftRows
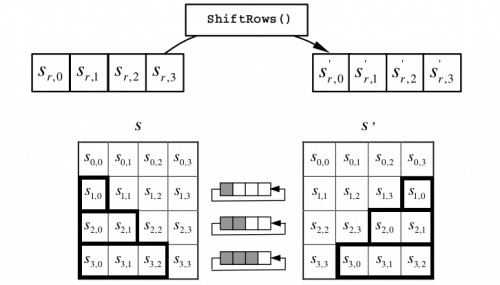
Source: Adapted from NIST (2001)
10-Stage MixColumns
The MixColumns step operates on the column-by-column State, and treats each column as a four-term polynomial (NIST, 2001, our translation), according to the following equation7:
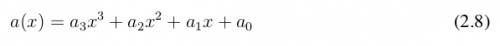
Columns are considered as polynomials and multiplied by modulus x4 + 1 with a fixed polynomial a (x) , given by the equation:
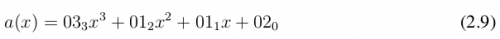
So the result of the step MixColumns over the State array, which is represented by s (x) , is the multiplication of the polynomial described in Equation 2.9 by elements of the State array s (x) which can be written as:
Being a (x) and s (x) the representation of Matrices, and elements of these matrices, it is possible to represent equation 2.10 in the form of a multiplication of matrices, as in the NIST article on AES, therefore, the representation equivalent can be seen in Figure 5 (NIST, 2001).
Figure 5-matrix representation for the MixColumns step
Source: adapted from NIST (2001)
With the result of this multiplication, the four bytes of a column are replaced, element by Element, as shown in Figure 6, just below:
Figure 6-elements to be replaced in the MixColumns step
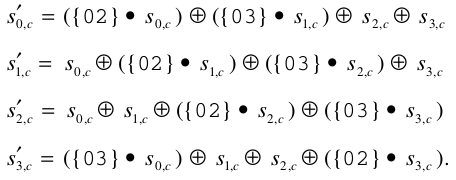
Source: adapted from NIST (2001)
After the number of the elements in s - 0,and c , o1,, c , o2,c, , and o3 a,c, array of the State, which together make up the column - c, they are replaced by the elements of s0,and c , s' - 1,, c , s' - 2,c, , and s3 a,c, , including the step of MixColumns, as shown in Figure 7.
Figure 7-step MixColumns
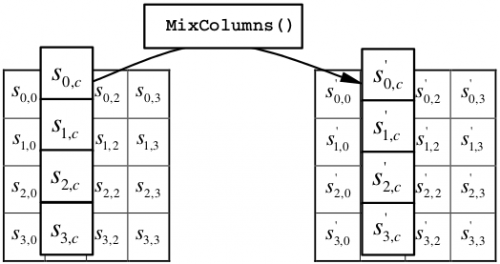
Source: NIST (2001)
11-stage AddRoundKey
The AddRoundKey step consists of adding a subkey to each byte of the array State, by means of a bitwise XOR operation (addition). The key is expanded each round using the AES key expansion, so that in each round a different key is used, derived from the original key, as seen in Figure 8.
Figure 8-step AddRoundKey
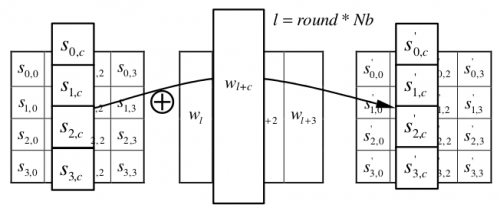
Source: NIST (2001)
12-decryption
The decryption consists of a process similar to that of encryption, but following the reverse order. The AES algorithm receives the encrypted content and if the key is the same as the one used to encrypt, the end result will be the original message. All AES operations are easily invertible. In a simple way, it is possible, for example, to rotate the columns to the original state in the ShiftRows step, or to know what the original byte by checking the row and column containing the byte in the step of SubBytes and reconstructing the Previous status.
Notes:
-
the original reference of the algorithm can be obtained through the link: http://csrc.nist.gov/publications/fips/fips197/fips-197.pdf
-
in the polynomial representation, multiplication in GF(28) (denoted by⊗) corresponds with the multiplication of polynomials modulo an irreducible polynomial of degree 8. A polynomial is irreducible if its only divisors are one and itself. For the AES algorithm, this irreducible polynomial is:
-
The modular reduction by m (x) ensures that the result will be a binary polynomial of degree less than 8, and thus can be represented by a byte. Unlike addition, there is no simple operation at the byte level that corresponds to this multiplication.
-
Non-linear substitution table used in several byte substitution transformations and in the Key Expansion routine to perform a one-for-one substitution of a byte value.
-
the SubBytes () transformation is a non-linear byte substitution that operates independently on each byte of the State using a substitution table (S-box). This s-box (fig. 7), which is invertible, is constructed by composing two transformations.
-
In the ShiftRows () transformation, the bytes in the last three rows of the State are cyclically shifted over different numbers of bytes (offsets). The first row, r = 0, is not shifted.
-
the MixColumns () transformation operates on the State column-by-column, treating each column as a fourterm polynomial as described in Sec. 4.3. The columns are considered as polynomials over GF(28 ) and multiplied modulo X 4 + 1 with a fixed polynomial a(x), given by:
Sources:
BOND, Martin et al. Learn J2EE in 21 days. [S. l.]: Pearson Education of Brazil, 2003.
Cormen, Thomas H. et al. algorithms: theory and practice . Rio de Janeiro: Ed. Elsevier, 2002.
Forouzan, Behrouz A.; FEGAN, Sophia Chung. Data Communication and network Computers . [S. l.]: McGraw-Hill, 2008.
KUROSE, James F.; ROSS, Keith W. Computer Networking and the Internet: a top-down approach . [S. l.]: Pearson Education, 2010.
RAPPAPORT, Theodore S. Wireless Communication: principles and applications . [S. l.]: Pearson Prentice Hall, 2009.
NIST. Announcing the advanced encryption standard (aes). Federal Information-Processing Standards Publication 197 , n. 197, P.51, 2001. Available in: csrc.nist.gov/publications/fips/fips197/fips-197.pdf>.
Thanks:
To the user mgibsonbr who initially answered this question and showed solidarity by removing my doubts in the comments and in the chat private. Very grateful! Without your knowledge and your solidarity, I would never have elaborated this answer and my knowledge about the AES algorithm (which is not yet complete and I still need to study a lot) would tend to zero.
In cryptography, the Advanced Encryption Standard (AES), also known as Rijndael, is a block cipher adopted as the encryption standard by the United States.
Is expected to be used worldwide and analyzed extensively, as was its predecessor, the data Encryption Standard (DES). The AES was announced by NIST (U.S. National Institute of Standards and technology) as U.S. FIPS PUB (FIPS 197) on November 26, 2001, after 5 years of a standardization process. It became an effective standard on May 26, 2002. In 2006, AES is already one of the most popular algorithms used for symmetric key encryption.
AES has a block size of 128 bits and a key with a size of 28, 192 or 256 bits, while Rijndael can be specified with keys and block sizes of any 32-bit multiple, with a minimum of 128 bits and a maximum of 256 bits.
The key is expanded using Rijndael key scheduling. Most AEs calculations are done in a finite field of their own. AES operates on a two-dimensional array of bytes with 4x4 positions, called a state (versions of Rijndael with a larger block size have additional columns in the state).
To encrypt, each turn of the AES (except the last one) consists of four stages (as already illustrated in the other answers):
AddRoundKey-each byte of the state is combined with the turn's own subkey; each subkey is derived from the main key using the key scheduling algorithm.
SubBytes - is a nonlinear substitution step where each byte is replaced by another according to a reference table.
ShiftRows-is a transposition step where each row of the state is shifted by a certain number of positions.
MixColumns-is an operation of merge that operates on the state columns and combine the four bytes of each column using a linear transformation. The final turn replaces the MixColumns stage with a new addroundkey stage.