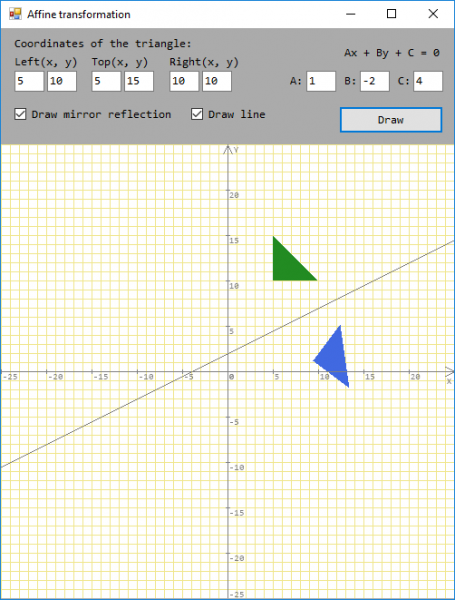
How to make a move relative to a straight line ax + by + c = 0, affine transformations
The task itself:
A triangle is set. Implement its motion based on the mirror reflection relative to an arbitrary straight line ax + by + c = 0, the coefficients of which are entered by the user.
What you've already done:
I read the coordinates of the three points of the triangle from the fields on the form.
Putting them in objects of the class Point (left(x, y), top(x, y), right(x, y)).
I make an array points from the points of the triangle:
Point[] points = new Point[3] { left, top, right };DrawField();
DrawCoordinateSystem();graph.FillPolygon(Brushes.ForestGreen, points);(as far as I understand, you just need to change the sign of all the points
Y)
I read the coefficients from the fields on the form(Point[] pointsCopy = (Point[]) points.Clone();for (int i = 0; i pointsCopy.Length; i++)pointsCopy[i].Y = -pointsCopy[i].Y;graph.FillPolygon(Brushes.RoyalBlue, pointsCopy);
a, b, c) for the equation ax + by + c = 0. Here's what happened:
Question:
Tell me how I can move it further relative to the straight line ax + by + c = 0 ?
4 answers
The point of the reflected triangle (polygon) can be calculated as follows:
x = A.x + (A.x - P0.x)
y = A.y + (A.y - P0.y)
Where,
|B*P0.x + C*P0.y, C|
|C*P1.x - B*P1.y, -B|
A.x = --------------------- ,
-B*B - C*C
|B, B*P0.x + C*P0.y|
|C, C*P1.y - B*P1.y|
A.y = ---------------------
-B*B - C*C
B = P2.x - P1.x
C = P2.y - P1.y
P0 - polygon point,
P1, P2 - points forming a straight line (ax + by + c = 0)
For detailed explanations about where these formulas came from, see my answer to a similar question
In such problems, it is easiest to work with a vector representation, it is very clear and accessible to the understanding of the head. You don't need to know any complicated calculation formulas, rotations, or matrices.
A this is a point, B - a vector, together they define a line from which it is necessary to mirror.
The formula for this line is: A + B * t
The point C and the vector D define a perpendicular line.
The point C is known from the condition, it is one of the points the triangle. The vector D is also known to be a vector perpendicular to the vector B, that is, it has coordinates By,-Bx, or -By,Bx, any one will suit us.
We make the equation of the intersection point
Ax + Bx * t = Cx + Dx * f
Ay + By * t = Cy + Dy * f
t and f these are the coefficients by which we multiply the vectors B and D to get to the intersection point, they are also our variables that we need to find.
Substitute instead of Dx,Dy the components calculated on the basis of B, that is, perpendicular to it vector.
Ax + Bx * t = Cx - By * f
Ay + By * t = Cy + Bx * f
We solve the equation and find the coefficient f. That's what we need.
Mirror point to point C, this is C + 2 * f * D
By coordinate
x = Cx + 2 * f * Dx
y = Cy + 2 * f * Dy;
From a "mathematical" point of view, to reflect a point (Px, Py) relative to a straight line A * x + B * y + C = 0 , you can do this:
-
We normalize the equation of a straight line, i.e. we divide all the coefficients of the equation by the length of the normal vector
(A, B). We obtain the normalized equationA' * x + B' * y + C' = 0 -
Calculate the signed distance from the point
(Px, Py)to the straight lineD = A' * Px + B' * Py + C' -
Moving the point
(Px, Py)to the distance2Dagainst the direction of the normal vector(A', B')Px' = Px - 2 * A' * D Py' = Py - 2 * B' * D
That's it - we got a mirrored point (Px', Py').
From a practical point of view, instead of pre-normalizing the equation in step 1, it is better to use non-normalized coefficients A, B and C and then just take into account the length of the vector in step 3 - this eliminates the need to calculate the square root to calculate the length and allows you to solve the problem in integers
D = A * Px + B * Py + C
L = A * A + B * B;
Px' = Px - 2 * A * D / L
Py' = Py - 2 * B * D / L
Here's how I figured out my task, maybe someone will need it.
To perform the reflection of a triangle relative to an arbitrary straight line, you need to perform specific actions:
- move the line and triangle so that the line passes through the origin;
- rotation of the line and triangle around the origin point to coincide with the X coordinate axis;
- reflection relative to the coordinate axis;
- reverse rotation around the origin;
- move to the starting position.
In matrix form, this transformation has the representation [T] = [T'] [R] [R'] [R^(-1)] [T'^(-1)],
where T' is the displacement matrix, R is the rotation matrix around the origin, and R' is the reflection matrix.
The equation ax + by + c = 0, can be reduced to the form:
by = -ax - c y = -a/b x - c/b
From it we find two points of the line A, B:
Point A = new Point( -width, -(a / b) * -width - c / b );
Point B = new Point( width, -(a / b) * width - c / b );
Where a, b, c - coefficients read from the fields on the form, width is the distance from the beginning of the canvas to the middle (width = Canvas.Width / 2), where x = 0.
As a result, there is a straight line L passing through the entire coordinate system.
Let's write it in matrix form:
float[,] L = new float[2, 3] {
{ A.X, A.Y, 1 },
{ B.X, B.Y, 1 }
};
We also write the matrix X from the array of points of the triangle points:
float[,] X = new float[3, 3] {
{ points[0].X, points[0].Y, 1 },
{ points[1].X, points[1].Y, 1 },
{ points[2].X, points[2].Y, 1 }
};
Now we do affine transformations using matrix multiplication.
For multiplication, we will use the method MultiplyMatrix
private static float[,] MultiplyMatrix(float[,] a, float[,] b)
{
float[,] product = new float[a.GetLength(0), b.GetLength(1)];
for (int row = 0; row product.GetLength(0); row++)
for (int col = 0; col product.GetLength(1); col++)
// Multiply the row of A by the column of B
for (int inner = 0; inner a.GetLength(1); inner++)
product[row, col] += a[row, inner] * b[inner, col];
return product;
}
1) To move the line and the triangle so that the line passes through the origin, we find the position y at x = 0:
float ys = -(a / b) * 0 - c / b;
Moving the line and triangle to the origin using the displacement matrix:
float[,] T = new float[3, 3] {
{ 1, 0, 0 },
{ 0, 1, 0 },
{ 0, -ys, 1 }
};
L = MultiplyMatrix(L, T);
X = MultiplyMatrix(X, T);
2) Rotate the line and triangle around the origin point until it coincides with the coordinate axis X. To do this, we find the angle at which the line is located relative to the X axis:
double radians = Math.Atan(-(a / b));
And rotate using the rotation matrix around the beginning coordinates:
float[,] R = new float[3, 3] {
{ Math.Cos(radians), -Math.Sin(radians), 0 },
{ Math.Sin(radians), Math.Cos(radians), 0 },
{ 0, 0, 1 }
};
L = MultiplyMatrix(L, R);
X = MultiplyMatrix(X, R);
3) We reflect the triangle relative to the coordinate axis using the reflection matrix:
float[,] Rr = new float[3, 3] {
{ 1, 0, 0 },
{ 0, -1, 0 },
{ 0, 0, 1 }
};
X = MultiplyMatrix(X, Rr);
4) Make a reverse rotation around the origin:
float[,] Rh = new float[3, 3] {
{ Math.Cos(radians), Math.Sin(radians), 0 },
{ -Math.Sin(radians), Math.Cos(radians), 0 },
{ 0, 0, 1 }
};
L = MultiplyMatrix(L, Rh);
X = MultiplyMatrix(X, Rh);
5) Move to the starting position:
float[,] Th = new float[3, 3] {
{ 1, 0, 0 },
{ 0, 1, 0 },
{ 0, ys, 1 }
};
L = MultiplyMatrix(L, Th);
X = MultiplyMatrix(X, Th);
Assigning new values for the array points:
for (int i = 0; i p.Length; i++)
{
points[i].X = X[i, 0];
points[i].Y = X[i, 1];
}
Draw a triangle with the new coordinates:
graph.FillPolygon(Brushes.RoyalBlue, points);