The problem of triangulating a polygon
A polygon is defined by the coordinates of its vertices along the circumference of its contour. You need to specify a set of diagonals that do not intersect at the inner points, dividing the polygon into triangles.
Input: file input.txt, , in the first line of which is written the number N – the number of vertices of the polygon, then in N lines of a pair of integers-the coordinates of the vertices of the polygon in the order of the contour traversal.
Constraints: 4 ≤ N ≤ 200; each coordinate from -10000 до 10000.
Output: file output.txt, in the first line of which there must be a number k indicating the required number of diagonals. The next k lines must contain two natural numbers – the number of the starting and ending vertices of the corresponding diagonal.
Additional restrictions: the diagonals must lie strictly inside the polygon (all points of the diagonal, with the exception of the ends, are internal points of the polygon).
Example:
input.txt
5
1 1
2 5
5 5
5 1
2 2
output.txt
2
2 5
3 5
My solution:
-
The number of diagonals is equal to (the number of vertices is 3)
-
Connect all points from (2) to (the number of vertices is 2) with the last point; if the line between the connected point and the last point lies outside the polygon (the polygon is non-convex), then take the next point and connect it to some (which?) dots.
Please help me to implement all this, or tell me how to check whether a straight line (or a point) belongs to a polygon and which points to connect if the polygon is non-convex.
2 answers
- If the number of vertices is
- Select the first vertex as the current one (N)
- If it is impossible to draw a diagonal inside the polygon to the point N+2, then the next one becomes the leading one, and so on along the ring. I think we can prove that this cycle is not infinite.
- "Cutting the "triangle" from the polygon, the vertices become one less due to the exclusion of the vertex N+1.
- Moving on to point 1
It's probably convenient to use svyazny list.
Determining whether a diagonal passes inside a polygon.
Let's determine in advance in which direction the polygon is set-clockwise or counterclockwise. Further, if the triangle N N+1 N+2 goes around in the opposite direction, then our diagonal outside is not suitable. Otherwise, another option is possible when the diagonal turns out to be completely or partially outside due to other internal angles, this is checked further.
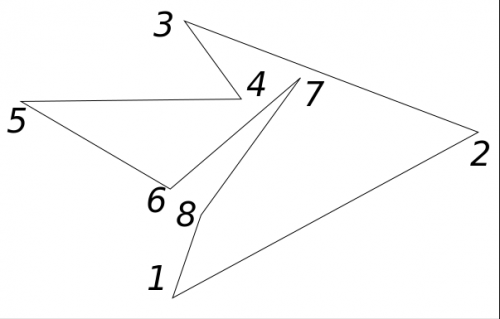
For points N+3 and N-1 you need to check that these angles at these vertices are greater than the corresponding angles of the triangle being cut. That is, the vertex lies on the other side of the diagonal relative to the vertex N+1, or the angle at the vertex is greater than the expanded one. (See the picture for vertex 2, the angle 2-3-1 is greater than 2-3-4, or 4 and 2 are on the same side of the diagonal 3-1, so the diagonal 3-1 is not suitable. For vertex 8, it is with vertex 6 on one side of the diagonal 7-1, but the angle 7 is larger than the expanded one, so it is not hinders, the vertex fits.)
For the remaining sides, check whether they intersect the given diagonal. (For example, in the figure, side 6-7 intersects diagonal 4-2. The intersection point of the lines belongs to the segment.) There are no four sides to check: these are the sides at the top and the ones adjacent to them.
Determining the direction of the polygon traversal
We draw from one vertex A1 of the vector to all the others A1->A2, A1->A3, ... A1->AN. Counting the sum of N-1 vector numbers products of neighboring vectors in order, we are only interested in the z coordinate. This sum is modulo twice the area of the figure, and the sign indicates the direction of traversal.
Optimization from @AnT: In order to determine the direction of the polygon traversal, it is enough to calculate the vector product of the sides of the incident with the lower-left vertex (the minimum x among the minimum y). There is no need to do this at all vertices (i.e. count the total area).
The classical algorithm for solving this problem is to perform two steps
- Decomposition of the original polygon into monotone polygons. This problem is neatly solved by the scanning line algorithm.
- Triangulation of each monotone polygon. This is done by a simple triangulation algorithm.
In the end, the resulting algorithm will be much simpler and more efficient than the "cutting off ears" algorithm with a hit check diagonals inside the polygon.