What is a context-free language?
In Wikipedia has the following statement :
In formal language theory, a context-free language (LLC) it is a language generated by some context-free grammar (GLC). Different context-free grammars can generate the same language context-free, or, conversely, a given language free of context can be generated by different context-free grammars.
Oh God!!!
However, I found the explanation a bit confusing, shuffled, and so I still ask:
- what is a context-free language?
- How is it possible, if it is possible, to define whether a language is context-free or not?
2 answers
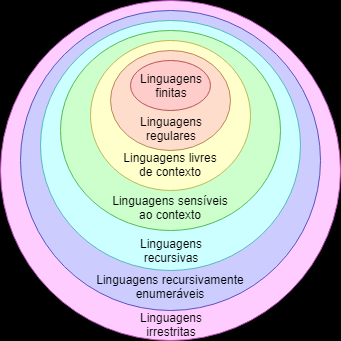
There is a hierarchy defined by Chomsky and refined by other researchers about structure of languages denoted by sequences of symbols, words, letters, etc. This structure contains the following levels:
Finite languages.
Regular languages - those of regular expressions.
Context-free languages-I'll explain below.
Sensitive languages context.
Recursive languages (also called Decidable).
Recursively enumerable languages (also called semi-Decidable).
Unrestricted languages - that is, this is the most general category that encompasses any and all languages.
Each level is a superset of the previous level. Thus:
Context-free languages are more powerful and more general than regular languages. That is, with context-free languages you can express structures/languages that cannot be represented by regular expressions.
All languages that can be expressed through a regular expression can also be expressed through a context-free language.
Context-free languages are still far from being languages capable of expressing anything. Exist a few levels above them.
The hierarchy looks like this:
Well, let's take a look at regular expressions first since you're more likely to have seen them before. For example, a regular expression of type ab(c*)(d|e)[f](g+) denotes sequences of symbols that have the following structure:
Start with
ab.Have zero or more
cs next.Have a
dor aenext.Then they may or may not have a
f.-
End with one or more
gs.
Well, we see that regular expressions can contain rules in the following formats:
Sequences of input string symbols.
Zero repetition or more times of subexpressions.
Repetition one or more times of subexpressions.
Choose from two or more subexpressions.
Optional Subexpressions (appear zero or once).
However, a regular expression is not recursive. A context-free grammar is a grammar composed of recursive rules called Productions. Each production is identified by a symbol / name called non-terminal . One of the non-terminal symbols is called the initial symbol, which is the starting point in the case of generation and the ultimate goal in the case of acceptance (more below I explain this better). In addition to the non-terminal symbols, we have the terminal symbols that correspond to symbols (characters) that are represented directly in the input string.
Context-free grammars may contain all of these elements that regular expressions have, but they have one more possibility. They can also:
- expand non-terminal symbols amid terminals, including non-terminal symbols that expand recursively.
To demonstrate, I will take as an example one of the grammars that is in the wikipedia article :
T →
x
T →y
T →z
S → S+T
S → S-T
S → S*T
S → S/T
T →(S)
S → T
An equivalent form of this grammar would be it:
T →
x|y|z|(S)
S → S+T / S-T / S*T / S/T / T
In grammar, and symbols x, y, z, +, -, *, /, ( , and ) is the terminal, and the symbols O and , T are the non-terminals. The non-terminal symbol S is the initial symbol. This grammar models arithmetic expressions (although it has no rules of precedence).
The set → is read as "drift " or"produce". Therefore, the Rule T → x can be read as "t drift x", or " t produces x". Note that in this given example, it is possible for a S to derive another s or for a t to derive another t directly or indirectly, since productions are applied recursively.
To see an example in practice, note that an expression such as x-(z)+(x*x) can be produced from the initial symbol S like this:
S // Símbolo inicial
S+T // Aplicação da regra S -> S + T
S+(S) // Aplicação da regra T -> ( S )
S+(S*T) // Aplicação da regra S -> S * T
S+(T*T) // Aplicação da regra S -> T
S+(T*x) // Aplicação da regra T -> x
S+(x*x) // Aplicação da regra T -> x
S-T+(x*x) // Aplicação da regra S -> S - T
S-(S)+(x*x) // Aplicação da regra T -> ( S )
S-(T)+(x*x) // Aplicação da regra S -> T
S-(z)+(x*x) // Aplicação da regra T -> z
T-(z)+(x*x) // Aplicação da regra S -> T
x-(z)+(x*x) // Aplicação da regra T -> x
The recognition process is the reverse:
x-(z)+(x*x) // Cadeia de entrada
T-(z)+(x*x) // Aplicação da regra T -> x
S-(z)+(x*x) // Aplicação da regra S -> T
S-(T)+(x*x) // Aplicação da regra T -> z
S-(S)+(x*x) // Aplicação da regra S -> T
S-T+(x*x) // Aplicação da regra T -> (S)
S+(x*x) // Aplicação da regra S -> S - T
S+(T*x) // Aplicação da regra T -> x
S+(T*T) // Aplicação da regra T -> x
S+(S*T) // Aplicação da regra S -> T
S+(S) // Aplicação da regra S -> S * T
S+T // Aplicação da regra T -> (S)
S // Aplicação da regra S -> S + T
Note that the process of generating or producing a string is the one that, starting from the initial symbol, reaches a sequence of terminals, while the process of recognizing or accepting a string is the one that starting from the string, reaches the symbol initial. These generation and recognition processes also exist for regular expressions, as I can use them both to generate and recognize strings.
Now, note that in the case of the above example, the generated and/or recognized expression will always have the parentheses balanced and properly nested, which regular expressions are not able to do. this demonstrates that context-free grammars are more powerful / expressive than regular expressions.
As for the difference between context-free languages and context-free grammars is that a grammar is what I posted above, a set of rules. On the other hand, a language is a certain set of strings of symbols that are accepted or generated, regardless of what rules are used to generate or accept them. A language that can be generated or accepted by a context-free grammar is a free language context. The same language can be generated or recognized by different grammars, which in this case are equivalent.
You may be wondering why this name is "context-free". The answer is that recognizing a subexpression does not depend on the context in which it is inserted. That is, it does not depend on what precedes or succeeds such underexpression. For example, a (sub)expression x-y can be recognized or generated as a S in the previous grammar regardless of what comes before or after that x-y. In context-sensitive languages (or languages that are even further in the hierarchy) this may not be true.
Finally, to define whether a language is context-free, you must demonstrate that there is some context-free grammar that recognizes it. To prove that it is not context-free, you must prove that there is no context-free grammar that recognizes it.
The answer from @Victor Stafusa is excellent, I just come here to deepen a few points.
Language
A Language is a subset (can be finite or Infinite) of words generated by the operator Kleene star over a set of symbols.
Word
A word is the concatenation of 0 or more symbols.
A word with zero symbols is the empty word. Could be represented by epsilon or lambda, or simply by "".
A single symbol is considered a word of size 1. Two concatenated symbols is a word of size two.
You can concatenate any desired word, even the empty word. I will represent the concatenation with the dot operator .. Some examples of concatenation:
"a" . "b" -> "ab"
"ban" . "ana" -> "banana"
"" . "" -> ""
"" . "a" -> "a"
"a" . "" -> "a"
Formally, every element formed by the Kleene star over a set of symbols T is a word formed by T.
Kleene Star
A Kleene star generates concatenations of words over a previously existing set of words.
But, Jefferson, you said right before that a language is a subset about of the set generated by Kleene's Star about symbols, why are you speaking that the star can operate on words?
Remember that more recently I wrote about size 1 words? Well, a single symbol is a word of size one, so these definitions do not go into contradiction.
The Kleene star operator is over a set V is represented by V*
A word is generated by the Kleene star over V if:
- it is the empty word;
- it is a word of
Vconcatenate of a word generated byV*.
Yes, the definition is recursive. More formally, the second step is given by the following mathematical expression:
Language as set
Language L is a subset of T*, being T a set of symbols. As a set, I can define in several ways. For example:
This is a word formed by symbols a, b and c, such that all as appear before all b, which in turn appear before c S. and also have the same amount of a s, b s and cs.
For some cases, the language needs to follow a structure, called the syntax . To define a syntax, a grammar is used. Unfortunately, set notation is poor for expressing the syntactic structure of one language, so we have another notation for this...
Derivative Grammar
Derivative grammar, or Transformational Grammar, was proposed by Chomsky to study in a structured way how natural language sentences are formed.
A grammar is defined as a set of symbol transformations. Usually, we have a transformation defined like this:
V -> W
Where V is a lexical form and W another lexical form.
What is a form lexicon?
Let's go back a little to Portuguese, our language. A reduced version of phrase formation would be:
- in general, we have a sentence
F -
Fcan be described asSVO, whereSis a subject,Vis an adverbial phrase, andOis an object -
Sis described by a nominal phraseSn - as well as
Ois also described asSn - a
Sncan be directly a nameN, but can also be a nominal phrase combined with an adnominal adjunctANbefore or after anotherSn - therefore, a
Sncan be represented byN,Sn . AnorAn . Sn - a
Anis an adjectiveAdthat can be combined by an adverbAvin the same way that a noun phrase is combined with adnominal adjectives - therefore,
Ancan be represented byAd,An . AvorAv . An - similarly, verbal syntagms are verbs
Veor combinations of verbal syntagms and adverbs:Vis represented byVe,V . AvorAv . V -
Nis the Union of the morphological classes of nounsSuand pronounsP -
Su,P,Ve,AdandAvare the grammar classes we study at school
I can turn these rules into a grammar as follows:
F -> SVO
S -> Sn
O -> Sn
Sn -> N | An Sn | Sn An
N -> Su | P
An -> Ad | Av An | An Av
V -> Ve | Av V | V Av
A lexical form is any concatenation of symbols, being able to contain intermediate and final symbols in any proportions. Examples of lexical form:
F
"verde"
Sn
"incolores" . "ideias" . "verdes"
Sn . V . Sn
"incolores" . Sn . Ad
"gato" . "amarelas"
A word is a special lexical form that is composed only of final symbols. Therefore, from the above examples, only the following are words:
"verde"
"incolores" . "ideias" . "verdes"
"gato" . "amarelas"
Note that the grammatical structure does not need to make the generated word make sense in the language used, since there is no semantic evaluation, only syntactic. An example of a meaningless thing is to have something ("ideas") that has one color ("greens") and has no color at all ("colorless").
The language generated by a grammar is the set of all possible words that can be generated with the grammar starting from an initial symbol; this language is indicated as L(G).
Grammar classification
As Victor Safusa has already said, there are several types of grammars. They are differentiated in how each production is made.
A grammar sensitive to context has the following form:
A V B -> A W B
A B -> B A
V -> Z
Note that V turned into W given the context A prefix and B suffixed. In counterpoint, note that V flip Z has no context involved. Production V -> Z is therefore said to be context-free.
A context-free grammar is a grammar whose productions are all context-free. To be context-free, the left side (producer ?) can only have a single non-terminal symbol, being free the right side (produced?).
As a curiosity, a regular grammar follows the following form, for V and W non-terminal symbols and a any terminal symbol:
V -> a W
V -> a
V ->
In Chapter 7 of my undergraduate monograph, I used context-sensitive grammars to demonstrate some simulated properties of petri Nets.
Context-free languages
A language is context-free if it is possible to describe it by a Context-Free Grammar. Simple as that, isn't it?
Well, then for it not to be free of context, it is necessary to demonstrate that it is not possible to build language, even with all the infinite possible Productions.
For a grammar to be infinite, one thing needs to be true: a non-terminal symbol needs to produce itself. In a crass way, it would be something like this (always doing the generation of the word from the symbol in parentheses):
S -> A(B)C -> AXT(Z)LC -> ... -> AXTPQO S AHFUQLC
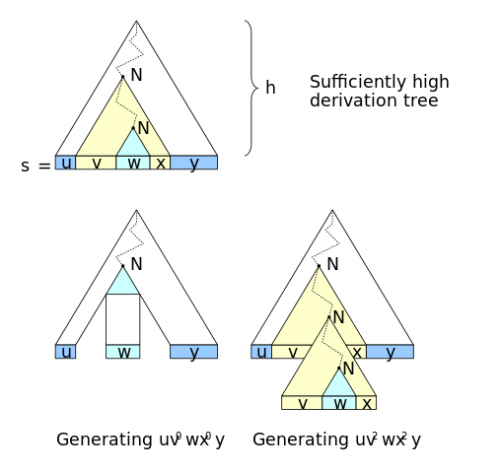
From the symbol S, I reached S again, preceded by AXTPQO and succeeded by AHFUQLC. This means that I can also get the lexical expression AXTPQO AXTPQO S AHFUQLC AHFUQLC, and also the AXTPQO AXTPQO AXTPQO S AHFUQLC AHFUQLC AHFUQLC, and generically (AXTPQO)^n S (AHFUQLC)^n. This operation (Exit Sand arrive at S again) is called pumping.
Visually, you have this image of the pumping motto on Wikipedia that shows the generalization of the paragraph previous (N pump N):
Every context-free language follows this motto of pumping when infinite.
EDIT an alternative name given to this pumping production is auto nesting;
Nit is nested within the productions ofN
Direct answers
What is a context-free language?
A generated language for a context-free grammar.
How is it possible, if it is possible, to define whether a language is context-free or not?
In general, it is enough to prove by writing a context-free grammar, but this task is not always trivial.
There are cases where it is impossible to know if a context-sensitive language is context-free. Even proving that a language is not Context-Free is difficult because even languages that respect the pumping motto may not be context-free.