What is a Turing stop problem?
I have read and re-read in Wikipedia , I have watched some 15 videos in English and Portuguese on this subject, I have read several articles on google, but I can not understand.
Why would it enter an infinite loop? Or why would she stop? All explanations using the contradiction do not make sense in my head.
Please without technical terms. Help me with simple logic to understand.
2 answers
What is a Turing machine for laymen?
A Turing machine is a minimalist mathematical model of a computer with an infinite memory. Although it is minimalist, all Turing machines are able to simulate each other. That is, all computers with infinite memory are able to simulate each other (even if the performance is lousy).
Therefore, once you have an unlimited amount of memory, you it can solve any computational problem, right? No!
The stop problem
The stop problem is the first problem that has been proven to be computationally unsolvable whatever the amount of memory available. To see why, Let's elaborate the stop problem like this:
I need a computer program (
termina) that is capable of inspecting the code of another computer program (P ) to determine if it enters or does not enter an infinite loop when it is given the input C. Theterminaprogram should output "Yes" or "No" in a finite time.
Let's assume that you will design the program termina with the programming language you want using the techniques you want. One way to check if P can enter an infinite loop with the input C is to simulate it with such an input and keep monitoring each individual memory state of P . If the program P repeats some memory state, then it safely entered an infinite loop, and the program termina responds "No". If the program P finishes its execution( stop), then surely it has not entered an infinite loop and the program termina responds "Yes". However, that's not all.
The program P can occupy more and more memory as it processes the input C, and even if/when it consumes the entire input, it still does not stop and continue consuming more and more memory(which remember is infinite, and therefore it can consume as much as it wants). In this way, it is possible that it will never stop and also never repeat a state of memory. With this, the termina program will need to be smarter than simply monitoring memory states seeking for a repeat or a completion of P .
If the program P consumes more and more memory infinitely, the program termina could see if that memory follows some pattern of repetition. However, this also does not work, because the program P is producing the digits of π infinitely and therefore there would never be a repetition in this pattern. The termina program could determine that after consuming a very large number (X) of memory cells, then P does not stop, but will that after x + 1 memory cells it would stop?
Example 1 of why the stop problem is difficult
The program termina can inspect the structure of the program P to determine if it would stop, but let's assume that the program P is the program collatz below*, written in Python:
def collatz(n):
while n != 1:
print(n)
if n % 2 == 0:
n = n / 2
else:
n = n * 3 + 1
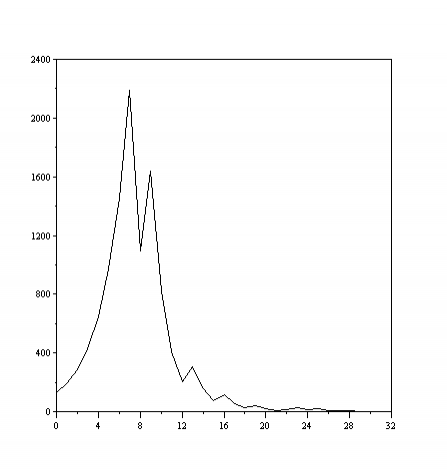
This is a very simple program. The value n is the input. When n reaches 1, the program terminates. If or n for even, it is divided by two. If it is odd it is multiplied by 3 and is added 1. It will print a sequence of numbers until n reaches 1. see here this program running on ideone for number 127. the image below shows a graph with the numbers generated in this process:
*:I took this program and also this image from Wikipedia
If I set a pretty large number to n, it will it stop by eventually producing 1? Or will it generate ever larger numbers indefinitely forever? The answer is that you don't know. This is a mathematical problem (Collatz conjecture) proposed in 1937 for which no solution is known, although it is believed that the answer is that it always stops. If your program termina is to determine if this program collatz stops, then termina is a program capable of solving this conjecture in a finite time. That means that termina would have to be programmed with techniques sophisticated enough to prove unsolved mathematical conjectures.
Example 2 of why the stop problem is difficult
Another example (also in Python):
def reversed_string(a_string):
return a_string[::-1]
def lychrel(n):
s = str(n)
if s == reversed_string(s):
print(s + ' é palíndromo!')
return n
m = int(reversed_string(s))
c = m + n
print(s + ' + ' + str(m) + ' = ' + str(c))
return lychrel(c)
In this example, the input is a number n. If n is a palindromic number (also called a capicua, that is, equal to itself back-to-front), it is returned. If not, from this number n, a number {[26] is produced]} which is n back-to-front and then the two are summed producing c which is used recursively as a new n until a palindrome is produced. To be clear what the program is doing, it prints on the output all these numbers that it generates. see here the program running on ideone for number 468.
Does the function lychrel end when the input is number 196? This is another open mathematical problem. A Lychrel conjecture it states that it would always end, but it is believed that this conjecture is false and that 196 would be the first counter-example of it. Again, since this is an open-ended mathematical problem, no one knows the answer, and after a few billion iterations that produce numbers with billions of Digits, a palindrome insists on not forming, but it is not known if eventually one would form with a trillion, a quadrillion, or a zillion iterations or if in fact it would never form. see here the program running no ideone for number 196.
If your program termina were to examine the program lychrel to determine (in a finite time) whether it ends with input 196, it would need to be able to either determine when it would end or else discover a reason why it would never end, and thereby solve another open mathematical problem. Again, to do this, this termina program would not be something simple.
Example by diagonalization of why the problem of stop is hard
And then we fall into proof by contradiction from diagonalization. Imagine that the program P was this:
import termina
def malandro(entrada):
if termina(malandro, 'não importa'):
while True:
print('Estou num laço infinito')
else:
print('Acabou')
This program is malandro. It consists of the following: knowing that the program termina determines if another program stops with any input, the program malandro uses the program termina to determine if it itself ends with the input 'não importa'. If termina determines that malandro stops, then malandro enters an infinite loop. If termina determine that malandro enters an infinite loop, then malandro ends.
That is, the program malandro, asks the program termina what it does and then does exactly the opposite! This means that there is no way the termina program will give the correct answer when it receives the malandro program as input. That is, either the program termina is incorrect or it may not end in a finite time.
In this way, it is shown that there is no way to construct the program termina that it performs both correctly and in a finite time. Any attempt to construct it will, at least in some pathological cases, either produce the wrong response or not produce response in finite time. Thus, an error-free and perfect version of the program termina it simply does not exist.
What if the program could answer that it fell into contradiction?
A possible (and naive) solution would be if the program termina observed that the program malandro uses its own program termina or else that it depends on contradictory conditions and with this, rather than responding "Yes" or "No", answer "impossible to determine".
That wouldn't work either. Let's assume that the program malandro2 has inside it a copy of the program termina, but with all variables and functions renamed and encrypted. The program termina would have to determine that there is a copy of itself within the program that he wants to analyze. And then the program would be this:
import copia_malandra_de_termina
def malandro2(entrada):
z = copia_malandra_de_termina(malandro2, 'não importa')
if z == 'Sim':
while True:
print('Estou num laço infinito')
elif z == 'Não':
print('Acabou')
elif z == 'impossível determinar':
print('Impossível determinar uma ova, acabou sim!')
else:
print('Haha, vai acabar do mesmo jeito')
That is, no matter how sophisticated the termina program takes to try to avoid contradiction, there will always be an even more sophisticated way to defeat it. This reaffirms the hypothesis that the termina program simply does not exist.
Other unsolvable problems
One way to prove that a problem is unsolvable is to reduce it to the stop problem. The way to do this is by contradiction. Let's say that sbrubbles is the name of our unsolvable problem and that we have some hypothetical library with a sbrubbles_solver program that somehow solves it. If you can create an algorithm that by using the program sbrubbles_solver is able to provide a solution to the stop problem then you get to this:
- if there is a program to solve the problem sbrubbles, then we can use it to create a solution for the stop problem.
- we know that we cannot create a solution to the stop problem.
- therefore, by modus tollens , we cannot create a solution to the problem sbrubbles.
Therefore, by means of this technique of reducing a problem Q to the stop problem, it is possible to prove that Q is an insoluble problem.
It is true that to elaborate an algorithm that in theory would solve the stop problem taking advantage of a hypothetical function/program that solves the problem Q may not be a simple task. However, this is exactly how many problems are shown to be unsolvable.
In particular, according to rice's theorem, determining whether any computer program has any non-trivial semantic property is an insoluble problem. By trivial property means those that are valid for all programs or for no programs (and therefore, non-trivia are those that are true for some and false for others). By semantic property is understood by properties about the behavior of the program. The reason for this being insoluble is that the program in question Can, in the same way as the program malandro, use the program that determines whether it itself contains such a semantic property to produce a contradiction. Therefore, it is an insoluble problem to design any algorithm to that tries to decide something about the behavior of another algorithm B without there being any error, limitation, or infinite loop in the algorithm a.
The stop problem is usually provided as follows:
Given a program and an input it accepts, will that program give me an answer? That is, Will he at some point stop his execution?
Obs.: I have all the time in the world, but not infinite time.
Apparently, the answer should be yes. But... this is not always the case. Sometimes the program goes into infinite loop. This can happen because the programmer that wrote it made a mistake, either because the programmer chose the wrong approach when dealing with the problem, or simply because the problem in question cannot be solved.
But are there problems that cannot be solved? Yes, there are. They are problems that, given an input, there is the possibility of the program going into infinite loop. No matter how good the program is. And it does not enter into infinite loop in a simple and trivial way no. Some problems, such as recognizing if a word belongs to an unrestricted grammar, or if given a finite set of arrays n x n it is possible to obtain the null array only by multiplying (with repetitions) the elements of this set, programs that solve such problems can enter recursions and never return to some previous state.
Now, answering the questions in the text... in the order I find most appropriate. And I'm trying to put the concepts as lightly as possible, but for the sake of corretude will come at times when I will need to be too technical. Whenever possible I will try to separate a concept in the " lay " part, and leave a more technical and mathematical explanation below or linked.
... why would she [Turing's machine] stop?
A Turing machine is a automaton . As such, the only thing she does is:
- read data
- write data
And it does this from an initial die, called input. In decision problems you need a "yes" or "no"answer. And this answer is only useful at the end of processing, when the Turing machine is stopped. The acceptance or rejection of the input can be done through a writing, but it is usually more useful to know whether it is in an acceptance state or not.
Why would it [Turing machine]go into infinite loop?
Because there are insoluble/Undecidable Problems. We @ Guilherme Bernal proposes a heuristic to look for cases to identify when a software goes into infinite loop in this question, but I pointed out a "trivial" case of programmer failure that he could not detect with his heuristic. I also pointed out another "uglier" heuristic that is lighter, but with less false positive for "infinite loop program".
(Spoiler alert: technical part started) an example of problem that is Undecidable is whether a word can be obtained from an unrestricted grammar.
An unrestricted grammar is a grammar that accepts productions of any kind. See more here, here .
In other words, this problem is w ∈ L(G):
-
wis the word we want to know if it can be obtained from the grammar -
Gis the unrestricted grammar in question -
Lis the "language function", which given a language, returns all words that can be generated from it
In infinite language grammars, computing L(G) in its completeness is... Infinity too. Maybe infinite times some non-null polynomial?
So there must be some way to check without having to list all the words, right? Well, that depends on the grammar.
In case of regular grammars, it is trivial. The first step, however, is to turn the problem into an automaton of deterministic finite states (see more here ). After that, it is only to feed the automaton with the word, and if it stops in a state of acceptance, the word belongs to the language. Otherwise, it does not belong to the language.
For context-free grammars, you could normalize to Chomsky's normal form and try to assemble the derivation tree by the ascending strategy. If you get the Non-terminal S at the top, then it belongs to the grammar, otherwise (found another non-terminal or found no answer at all) so it does not belong.
For context-sensitive grammar, the thing starts to get complicated. There is no direct path to follow. The most we can do is turn it into a non-retraining grammar. Every context-sensitive grammar can be transformed into a non-retracting grammar so thatL(Gsc) = L(Gnr), where Gsc is the context-sensitive grammar and Gnr is the non-retracting grammar. An interesting property of grammar non-retraining is that a Sentential form can only be derived into Sentential forms of the same size or greater. So if the intermediate Sentential form is greater than the length of w, we already know we're on the wrong path, so just go back and try another path. And, yes, the solution for more efficient context-sensitive grammars is by listing in depth all possible transformations and cutting when the intermediate form is too large.
For grammars unrestricted... well, they can be written in such a way as to be retractive... even there is nothing prohibiting the consumption of a terminal generated in the middle of a production. So limiting by the size of the Sentential form is not a good one for the general case.
What to do in that case? Well, the best thing that can be done is to build the lead graph. This same graph can be used for the other restricted grammars as well.
How does this graph work? Well, we start with the vertex with the initial Non-terminal, S. So we check what are the productions that this Vertex can undergo, and for each production we take the vertex P1, P2... Pn for each of the n possible Productions and we connect with edges to the originator Vertex. If one of the productions generates an already known Sentential Form Pi, we must connect to this vertex instead of creating a new Vertex. Then we add all the vertices in the structure of future visits and Mark S as already popular.
The next step is to take the next vertex of the future visit structure and, on top of it, make all possible leads, add the new vertices and New edges in the graph, adding the neighboring vertices in the future visit structure to then mark the vertex as visited. Of course, if a vertex has already been visited, one should not do this processing again.
If the vertex being visited is composed only of terminals, then we can check se Pv = w. If yes, we find the answer, otherwise we do not know anything.
In the case of non-retracting grammars, the proper structure for storing future visit vertices is stack, doing a deep search. This is because it is known that since the grammar is non-retracting, there is a maximum limit of vertices that can be generated in the middle of the way. If there are non-terminal n, I just need to examine at most (n+len(w))^len(w) distinct vertices, as there are n+len(w) distinct symbols in grammar that are relevant to the word w and any Sentential form Pg such that len(Pg) > len(w) implies that w cannot be obtained from Pg.
In the case of unrestricted grammar, the best structure to do this analysis is the queue. This will allow you to do a search in width of the lead graph. Using the search in width avoids falling into a hole of doom that even exploring the infinite possibilities of it does not reach in w, for the processing of other paths continues to be done.
If it is possible to answer "yes", occasionally in one of the vertices it will contain w and we will surely pass through it from here until the end of time. If this is not possible, there are two hypotheses:
- all paths have been investigated to the end, so grammar generates a finite language
- at least one of the paths is an endless well and the program will continue to explore that well in width, adding new vertices to be visited
In the second case, the Turing machine will not stop.
All demonstrations using contradiction don't make sense in my head.
Well, I think that means that you have doubts about how to prove that the stop problem is undecidable. Let's use the previous problem to clarify this?
If you, dear reader, have skipped the previous section after viewing the spoiler alert: technical part started , I will briefly recap what the problem is. One wants to know if a word w can be generated from an unrestricted grammar G. We then model a graph that represents all the Sentential forms that I can get from a previous Sentential form by obeying the production rules of G and do a width search.
The possible results are:
- if
wcan really be generated byG, after" some " processing we will findw - if we try to walk in width all the paths and they ended up without finding
w, then the languageL(G)generated byGwas finite and we enumerated all its elements and none of them wasw - one of the paths is an endless well, in which the search in width will continue indefinitely generating new vertices in vain, without ever leading to
w
We know these results why in a certain way we know a priori if w ∈ L(G). And what would happen if we didn't really know the result of the algorithm?
In this case, we will need to wait for the algorithm to give an answer (1), enumerate all the possibilities, and none of them is w (2), or for it to go into infinite loop (3).
Cases (1) and (2) are trivial. After all, if it stopped, it stopped, we have the answer. And for the case (3)? @ Guilherme Bernal provided a heuristic in this question . But unfortunately it does not work for the general case.
Looking from another perspective... I will leave my Turing machine working for a while. I leave her suing for... two weeks. After that time I pause it and check its internal state. Well, she says there are still paths to be cleared, vertices not visited. Then I'll let her process a little more. I'll be back five years later, so what? Well, now there are two billion vertices to be visited. I'm scared, but that it means that she is progressing... or not?
Well, maybe the next second she just stops and yells " I'm done, I found w". Maybe it'll take another week. Or two centuries. Impossible to determine this by looking at her. Maybe these two billion vertices are two billion endless wells. Or not! Maybe all of them will be able to generate w in the near or distant future. maybe the processing is leading somewhere, maybe it's just processing in vain.
By taking a Turing machine that solves the problem of whether w is generated by G and it is still in processing, it is impossible to determine whether it is because it is on its way to (1) or (2), or if it is in perdition at (3).
This is an example that shows the impossibility of determining whether a given Turing machine will one day give an answer. After all, I have all the time in the world, but not infinite time.