It is difficult to summarize much since there are many concepts that need to be mastered to correctly understand Karnaugh's map. Below I will try to simplify to the maximum without leaving important details out.

Summary

• the Karnaugh map is a systematic method for simplifying logical expressions;
• can be used to simplify logic circuits, abbreviate Boolean expressions, convert expressions of different formats, between other;
• is directly related to the truth table so knowing it is trivial;
• grouping 1 on the map will generate output in the sum of products format;
• grouping 0 on the map will generate an output in the sum product format;
• you should always choose to group by the most present value on the MAP;
• groups should always be formed in power size of 2, as large as possible;
• groups should be formed only by adjacent values;
• all values must belong to at least one group;

Introduction

The Karnaugh map - sometimes called a diagram - is a technique for simplification of Boolean expressions, arising basically to counteract the techniques of simplification through Boolean algebra, which are exhaustive, require deep knowledge of all the rules and very easy to get wrong; in turn, simplification through boolean map {[ Karnaugh's is a systematic method by simply following all his steps to get the result.

Is a concept very related to the truth table, since it is customary, in practice, to elaborate the Karnaugh map from the truth table, given the ease that this brings the solution and the ease of constructing the truth table the part of any Boolean expression.

What is a "truth table" and what is it for?

The result of Karnaugh's map, when executed correctly, it will always be the simplest expression in the product sum or product sum formats, depending on how the map is resolved, both non-canonical.

Application

The Karnaugh map can be used to simplify any Boolean expression, that is, when you are developing a logical circuit you can first make it work, without worrying too much about numbers of logical ports used and then apply the Karnaugh map to the system and maximally reduce its circuit, thereby decreasing, design cost, response delay and electrical power consumed. Another possible application is the reduction of logical operations performed by UI to check an expression in your code. If you have a if with an overly complex expression, you can use Karnaugh's map to simplify it.

Construction and Resolution

Karnaugh's map works great for logical expressions with 2 to 5 vary. Above that the resolution of the map ends up becoming too exhaustive and generally makes its use unfeasible. As an example for the answer, we will always consider the letters of A to E as being the variables of the logical expression and S as being the output value.

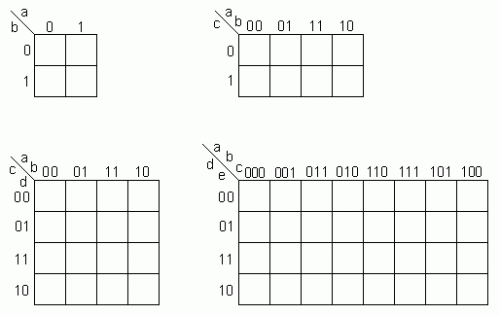
To build the map for an expression with n variables, you will need to build a table with 2^n cells, in the following format:

1. for n = 2, a table with 2 rows and 2 rows is created columns;
2. for n = 3, a table with 2 rows and 4 columns is created;
3. for n = 4, a table with 4 rows and 4 columns is created;
4. for n = 5, a table with 4 rows and 8 columns is created;

Note that for n > 2 you will need to create groupings of the input. On the first map, the values of A are placed in a row and the values of B and column; on the second map, the values of combination AB are placed in a row and the values of values of B in column; in the third map, the values of the combination AB are placed in line and the values of the combination CD in column; in turn, in the fourth map, the values of the combination ABC are placed in line and the values of the combination of in Column. The combinations that will be placed in row or column does not matter much, but it is a matter of life and death you correctly position the values. These must always follow the order of Gray, that is, each value of the row or column should only vary by one bit for adjacent rows or columns. Notice that in the second map, the combination AB is positioned in the sequence 00, 01, 11 and 10, because if it were in the natural order, 00, 01, 10 and 11, between the values 01 and 10 there would be the change of two bits and this is not allowed. This is actually the essence of Karnaugh's map. This process would be the equivalent of you placing the terms with the most variables in common side by side in Boolean algebra, thus simplifying the process.

Each cell of the Karnaugh map is referring to a cell of the truth table and must be filled in as such. After completing the map, it should be checked if there are more zeros or ones, because to obtain the most simplified form of the final expression, one should always consider the values in greater quantity. If there are more zeros than zeros, you will Group them and get an answer in the formed sum of products; if there are more zeros than zeros, you will Group them and get one answer in the product format of sums. Also, another application of Karnaugh's map is the conversion between the sum of products format to sum product, or vice versa. The grouping should always be done considering power quantities of 2, obtaining the largest possible groups. The only rule for grouping, besides the size being power of 2, is that the values of the group must be adjacent to each other in the row or column, considering the table as a cylinder, that is, the first row it is considered adjacent to the last, just as the first column is adjacent to the last. Once the grouping is done, each group will generate an operand of the result and this operand will be defined according to the variables that keep their value within the respective group. This will become clearer in the example.

Example

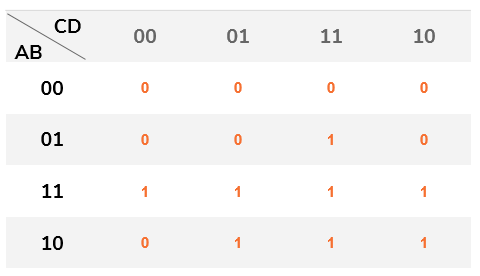
For a practical example, let's consider that the program will calculate a mathematical process of 4 distinct ways in parallel, returning the result when at least three processes have been terminated with the same value, or when two of them terminate, one of which is process A. That is, if all processes ABCD terminate, if BCD terminate, or if AB, AC or AD terminate, the program must return the result.

The canonical logical expression for this check would be:

S = (A.B.C.D) + (~A.B.C.D) + (A.B.C.~D) + (A.B.~C.D) + (A.~B.C.D) + (A.B.~C.~D) + (A.~B.C.~D) + (A.~B.~C.~D)

This requires the performance of 41 logical operations. Can you imagine writing a if with all this? But assembling the truth table, we have:

| A | B | C | D | S |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | -> B.C.D
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | -> A.D
| 1 | 0 | 1 | 0 | 1 | -> A.C
| 1 | 0 | 1 | 1 | 1 | -> A.C.D
| 1 | 1 | 0 | 0 | 1 | -> A.B
| 1 | 1 | 0 | 1 | 1 | -> A.B.D
| 1 | 1 | 1 | 0 | 1 | -> A.B.C
| 1 | 1 | 1 | 1 | 1 | -> A.B.C.D

Ao build Karnaugh's map, we get something like:

We have the same amount of zeros and ones on the map, so it will be indifferent which one to group. By way of example, I will do both ways.

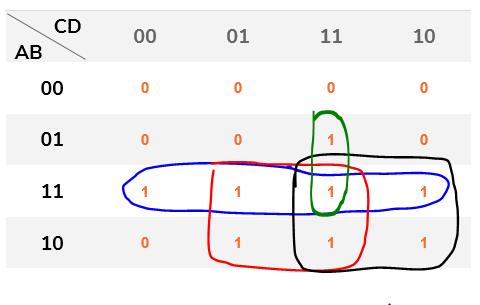
Groups of 1

First, let's solve the map by grouping them together to get the answer in sum of products. The possible groups are:

It is worth remembering that all values must be grouped and that a same value can be part of several groups. In this way, analyzing each group, we have:

• Blue: variables A and B have the same value throughout the group, so the generated operand will be a. B;
• Red: variables A and D have the same value throughout the group, so the generated operand will be a. D;
• black: variables A and C have the same value throughout the group, so the generated operand will be a. C;
• Green: variables B, C, and D have the same value in the whole group, then the generated operand will be B. C. D;

So the simplified expression will be:

S = (A.B) + (A.C) + (A.D) + (B.C.D)

Which will require only 8 logical operations, against the initial 41.

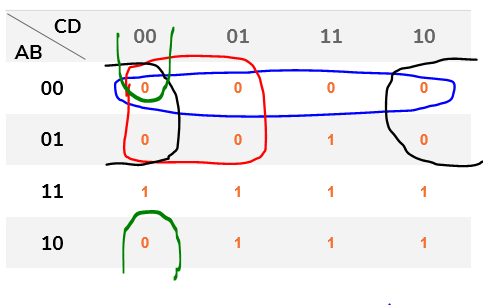
Groups of 0

The same can be done by grouping the zeros:

Getting like this:

• Blue: variables A and B have the same value throughout the group, so the generated operand will be A + B;
• red: the variables A and C have the same value throughout the group, so the generated operand will be a + C;
• black: variables A and D have the same value throughout the group, so the generated operand will be A + D;
• Green: variables B, C, and D have the same value throughout the group, so the generated operand will be B + D;

So the simplified expression will be:

S = (A+B).(A+C).(A+D).(B+C+D)

Which will also require only 8 logical operations.