What is the NPI complexity class?
Studying about complexity, I came across the term NPI. It means NP-intermediate. But I did not understand what this "intermediary"is.
- What characterizes an NPI problem? Why does she have that name?
- is there a difference between NPI and NPC?
- does anything change in relation to this class if the answer to the problem is found P vs NP ?
- more about NPC and P vs NP: what is an NP problem complete?
- Mini-glossary to help with the search (more details in already existing @ VictorStafusa answer ):
- NP : non-deterministic polynomial
- P : polynomial deterministic
- NPC : NP-Complete
- NPI : NP-Intermediate
1 answers
The problems P are those that admit deterministic solution in polynomial time.
NP problems are those that admit solution Not-deterministic in polynomial time (that is, if you see a possible answer in a crystal ball, you can check whether or not it is correct in polynomial time).
NP-complete problems (NPCs) are the "most difficult of NP", reducing in polynomial time to each other. There are several known NP-complete problems out there, such as satisfiability, traveling clerk, Hamiltonian way, etc. If one of them is shown to be in P, then all NP problems would be in P and with that P = NP.
However, taking the premise that P ≠ NP, comes the question: are all problems that are in NP necessarily in P or in NPC? Or would there be problems in NP that are not in either of these two categories? That's where the NPI comes in.
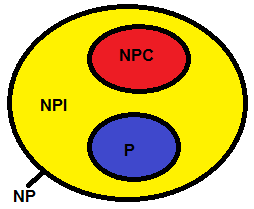
The NPI class corresponds to the set of problems that are in NP, but are neither in NPC nor in P. These are problems for which there is no deterministic solution in polynomial time (they are not in P), but still a possible solution can be checked in polynomial time (they are in NP) and are not NP-complete:
Richard Ladner demonstrated in 1975, that if P N NP then there are problems within NP that are neither in P nor in NPC, it was with him that the NPI class arose. She has this name (intermediate NP) because they are neither the hardest of NP (NPC) nor the easiest (P). Therefore, they are in an intermediate category.
No real problems are known that are definitely in NPI. Not least because if to prove that a problem is NPI, you would have to prove that it is in NP, but it is out of P, and with that you would have to prove first that P ≠ NP before proving that some particular problem is in NPI. Despite this, there are some suspicious problems of being in this area, the most famous are:
- Number factorization
- discrete logarithm
- graph isomorphism
Let's take the factorization problem:
Let x be the number you want to factor. If you see in a crystal ball a sequence of prime numbers that supposedly multiplied result in x , you can easily do the multiplication and check whether or not they actually produce x , soon this problem is in NP.
-
No efficient algorithm for factoring large numbers is known. Assuming that in fact none exists, then this problem is not in P.
There is no known way to reduce the satisfiability problem to the factoring problem in polynomial time, and assuming that such a reduction does not exist, the factoring problem is not NPC. In fact, NPC problems seem to be significantly more complex than that of factorization.
So, if these assumptions are true, the factoring problem is NPI.