Why is log N used to calculate the complexity of algorithms instead of lb N?
In all sources, the complexity of the algorithms is denoted as log N (without specifying the basis). In this case, we mean the logarithm in base 2.
But for such a logarithm, there is a notation lb. Moreover, this designation is standardized ISO 31-11 and it would probably be more logical and correct to use it, but this for some reason does not happen, why?
UPD: I don't have any math education and everything I know about logarithms, which is the inverse of exponentiation.
Let's take a specific example - binary search. Everywhere describe its complexity as log N. At the same time, log N, as it seems to me, still means the logarithm of N on the basis of 2, since the number of operations is exactly the logarithm of N on the basis of 2, i.e. to what degree should we raise 2 (and not 10 and not 100) to get N. So, to be honest, I don't understand answers like " because the constant coefficients in the notation O(n) do not have the value " or " since the entry with a large O does not react to constants - it does not matter which logarithm to use..." and I would appreciate a more detailed answer, written not for mathematicians. Does the rule that" constants in O-large do not matter " refer to the base of the logarithm? Doesn't it make any difference for a binary search how to write its complexity-logarithm by base 2 or by base 100?
If log N for binary search means exactly the logarithm of base 2, then why not write it as lb N, since there is a notation for the binary logarithm, instead of writing it without specifying the base at all?
UPD 2: I understand that " O(N) is by no means the number of comparisons, it is an estimate of the running time of the algorithm, as much as possible untethered from the details of the implementation and the machine."
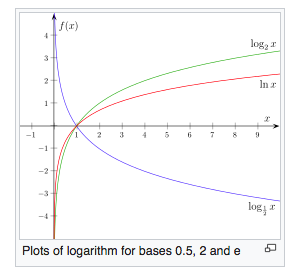
But here this: "And since the entry with a large O does not react to constants-it does not matter which logarithm to use ..." I do not understand. Why doesn't it matter which logarithm to use? Here are the graphs of the three logarithms - binary, natural, and base 0.5:
Let's take the same binary search. How can we replace the base of the logarithm from two to ten in its complexity? And from two to 0.5? I think we can't. I.e. we can't substitute log N in the expression an arbitrary basis because the dependence will be completely different - this is clearly visible on the graph. So what kind of logarithm is important to use. Or am I wrong?
2 answers
Since all logarithms are the same up to a constant :)
And since a record with a large O does not react to constants , it does not matter which logarithm to use...
Update to your question update.
The point is not in the specific number of comparisons, but in how this number grows (and hence thetime of work) with the growth of N. This is by no means a specific number of certain operations! What some the algorithm has a complexity of O (g(N)) just means that if we experimentally construct a certain function of the dependence of the algorithm's running time on N and get a certain f(N) , we can find some such constant c and N0, that for all N>=N0 the inequality 0 will be satisfied. This is the definition of a record with a large O.
Once again-O(N) is by no means a quantity This is an estimate of the running time of the algorithm, as much as possible untethered from the details of the implementation and the machine.
Update 2
I'm implementing a binary search algorithm and I'm terribly stupid, so instead of making one comparison, I make 20 of them. You do them exactly as much as you need. But both your and my implementations will run time O (log N) - even though mine will run 100 times slower than yours. Because both my and your implementations will run longer when N increases by 100 times for some time - even if everyone has their own, say, you have for a minute, I have for an hour. The main thing is that the type of dependence will be the same - with an increase of some times, the growth will be by some.
And by the way, you have dependencies log2x and ln x are exactly the same - you only need to change the scale slightly on the y axis. As for the logarithm on the base less than 1-well, as they say, do not exaggerate. But even here-it is enough to take it modulo or a negative constant :)
By the way, check out a few links here.
I think I found the answer to my original question:
"In all sources, the complexity of the algorithms is denoted as log N (without specifying the basis). In this case, we mean the logarithm in base 2. But for such a logarithm, there is its own notation lb. Moreover, this designation is standardized by ISO 31-11 and it would probably be more logical and correct to use it, but this for some reason does not happen, why?"
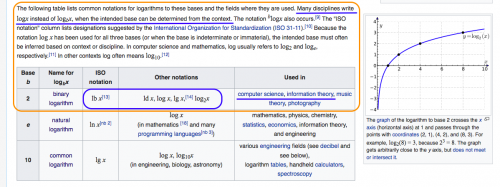
Here here: https://en.wikipedia.org/wiki/Logarithm#Particular_bases
I.e., for example, in computer science, log N is used instead of lb N or log N for a specific reason, because the base of the logarithm is clear from the context.
Perhaps the base of the logarithm doesn't matter at all when it comes to O-large, as @Harry replied. But, to be honest, my mathematical knowledge at the moment is not enough to give this statement an assessment. So I'd prefer for now a more general statement about the fact that "the basis is determined by the context"
UPD: I came across in one of the books on algorithms (just in the binary search section) the phrase: "Is it log base 2, log base 10, or the natural log? In the above example, log base 2 applies. However, since Big O notation only concerns itself with the shape of the performance the actual base doesn't matter." So, yes, it looks like the base of the logarithm is not important )